Abradatabra est une bande dessinée de vulgarisation réalisée dans le cadre du cours Critical Data Studies.
Elle discute des biais de perception que peuvent induire des manipulations graphiques trompeuses et des pièges rencontrés lors de l'interprétation de données, dans le but mieux comprendre ces visualisations que l'on rencontre au quotidien.
Pour les personnes envieuses d'en savoir plus, chaque épisode est accompagné d'explications plus détaillées sur les concepts abordés, ainsi que quelques points-clés de recommandations.
Sur ce, nous laissons Raymonde et Hugues vous faire découvrir ce monde, et vous souhaitons une agréable lecture !
Episode 1 - Tout un fromage

Deux producteurs de fromages ont un accident de charrue, et c’est toujours la faute aux mêmes personnes… enfin, c’est ce qu’on pourrait croire à première vue ! Cette planche met la lumière sur deux constructions graphiques et les pièges venant avec l’interprétation de pourcentages.
Comment comparer efficacement des pourcentages ?

En voyant la visualisation de Raymonde avec les trois graphes camembert, on se rend compte que la part du camembert représentant les accidents impliquant des charrettes à chevaux augmente d’année en année. Est ce que pour autant c’est de “de pire en pire” ? Non, puisque le nombre d’accidents au total diminue aussi !
Ce type de visualisation n’est pas intuitif, car il faut en permanence se rappeler que l’on compare des pourcentages, et non des valeurs absolues, ce qui défie le principe même de la visualisation graphique : autant mettre les pourcentages dans un tableau!
En solution, Hugues propose d’utiliser des camemberts de tailles différentes pour visualiser le nombre total d’accidents. Plus précisément, la surface de chaque camembert est proportionnelle au nombre d’accidents eus pendant l’année représentée.

Présenter ce même nombre par le rayon du camembert serait pousser à induire en erreur, il est intuitif que la quantité d’encre déposée (la surface totale) soit proportionnelle à la valeur numérique, or la surface d’un cercle grandit comme le carré du rayon : A ∼ r². En utilisant le rayon, on aurait alors tendance à surévaluer la valeur représentée.
Cependant, la littérature scientifique met en garde contre les visualisations basées sur des cercles. Dans How Numbers are Shown: A Review of Research on the Presentation of Quantitative Data in Texts, Michael MacDonald-Ross compile plusieurs études et montre que l’on a tendance à sous-estimer les surfaces des disques, biais aggravé par la taille du disque. La surface perçue suivrait une loi [surface perçue] = [surface réelle]^0.86.

En plus d’avoir tendance à être sous-estimées, les surfaces de disques sont difficilement comparables. Difficile d’inscrire mentalement un disque dans un autre pour comparer leurs surfaces, avec qu’avec des rectangles de base égale, il suffit de comparer les hauteurs.
Hugues propose alors d’empiler les fromages pour former un diagramme à bandes (“bar chart”), qui permet de représenter la même information, ainsi que de facilement comparer les données entre les années.
Faut-il abandonner le camembert ?
Faut-il pour autant abandonner le camembert ? Prenons un exemple de données fictives, par exemple celles dans le tableau ci-dessous. On pourrait imaginer que ces données correspondent aux vente journalières de différentes marques de glaces dans un magasin de votre choix.
| cat. 1 | cat. 2 | cat. 3 | cat. 4 | cat. 5 | cat. 6 | cat. 7 | |
|---|---|---|---|---|---|---|---|
| jour 1 | 9 | 6 | 5 | 2 | 2 | 1 | 0 |
| jour 2 | 9 | 6 | 7 | 3 | 5 | 3 | 1 |
| jour 3 | 10 | 7 | 10 | 3 | 7 | 4 | 5 |
| jour 4 | 12 | 10 | 11 | 8 | 9 | 5 | 5 |
Comment représenter ces données pour qu'on puisse les comprendre intuitivement ?
| cat. 1 (% jour) | cat. 2 (% jour) | cat. 3 (% jour) | cat. 4 (% jour) | cat. 5 (% jour) | cat. 6 (% jour) | cat. 7 (% jour) | |
|---|---|---|---|---|---|---|---|
| jour 1 | 36 | 24 | 20 | 8 | 8 | 4 | 0 |
| jour 2 | 26 | 18 | 21 | 9 | 15 | 9 | 3 |
| jour 3 | 22 | 15 | 22 | 7 | 15 | 9 | 11 |
| jour 4 | 20 | 17 | 18 | 13 | 15 | 8 | 8 |
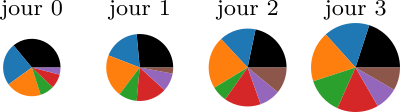
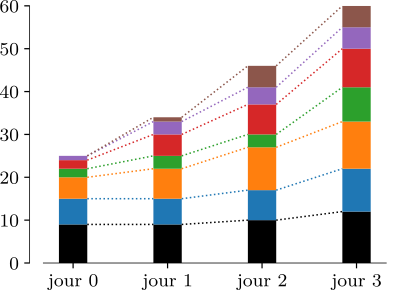
Edward Tufte explique dans le chapitre 8 de The Visual Display of quantitative Information que les camemberts ont une faible densité de données, et qu'il est préférable d’utiliser un tableau, plus précis, pour présenter des petits jeux de données. Pour des plus grands jeux de données, un diagramme à bandes est recommandé.
Cependant, selon l’étude Displaying proportions and percentages de Spence et Lewandowsky, les camemberts sont légèrement plus aptes que les diagrammes à bandes quand il s’agit de faire des comparaisons (groupées ou non) dans un jeu de données ; et cet effet est d’autant plus prononcé que le jeu de données est grand. Les tableaux, bien que précis, ne permettent pas d’exploiter son intuition géométrique, et ressortent inférieurs dans ce contexte.
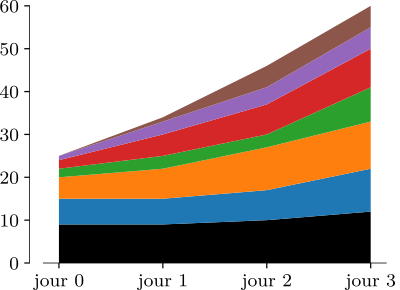
Ce que le camembert ne permet pas de faire, c’est des comparaisons entre jeux de données. Les positions des parties en désarroi forcent les yeux à sauter de camembert en camembert, tout en cherchant où se situe la partie à comparer. Dans ce type de situation, il est préférable d’utiliser un diagramme à bandes, qui permet à la fois d’afficher le total (si nécessaire), et de tracer des lignes entre les étages pour guider la lecture. Ou encore, si la situation s’y prête et l’encre n’est pas une limitation, on peut remplir entre les guides de lectures.
Points clés
- Attention lors de la comparaison de pourcentages entre jeux de données, prêter attention aux valeurs absolues.
- On a du mal à correctement estimer les surfaces. Utiliser des marqueurs linéaires (rectangulaires) plutôt que circulaires pour indiquer une magnitude.
- Pour comparer des pourcentages dans un même jeu de données, un camembert permet une meilleure estimation.
- Pour comparer entre jeux de données, utiliser un diagramme à bandes (avec ou sans guides de lecture).
Lien vers les données brutes et génération de graphes pour l'épisode 1.
Erratum
Episode 2 - Schifahren sur la mauvaise pente


Cette planche aborde des aspects vus souvent dans des thèmes politisés. Ce choix est motivé par le fait que la politique est un domaine où les graphiques sont omniprésents et utilisés pour manipuler ou orienter l'opinion en faveur du candidat.
Pour contexte, il s'agit des élections municipales du village. D'un côté, le personnage récurrent Raymonde, vu dans le premier épisode, et un nouveau personnage Schifahren, qui vient avec le projet de construire des pistes de ski artificielles accessibles en toute saison. Afin d'avoir une certaine continuité entre les épisodes, nous avons choisi que le nouveau candidat souhaite remplacer les alpages pour mettre en œuvre son plan. Il utilise trois manipulations graphiques trompeuses pour accentuer ses propos.
Des axes qui commencent à zéro et une pente trompeuse
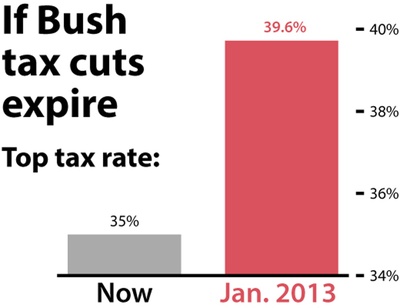
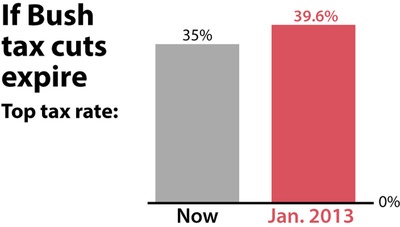
Pour ce premier point, une situation réelle a servi d'inspiration. En juillet 2012, Fox News a rapporté que le président Barack Obama prévoyait de maintenir les réductions des taux d'imposition fédéraux beaucoup plus élevés du président George W. Bush, qui expirent à la fin de 2013. Pour présenter les chiffres, un graphique a été montré à la télévision. Le graphique suivant est une reproduction, identique à l'original, qui se trouve dans How charts lie: getting smarter about visual information de Cairo. Notez que l'augmentation des impôts était d'environ 5 %, mais que les barres ont été présentées d'une manière qui les a exagérées.
La personne qui a conçu ce graphique a enfreint un principe de base de la conception de graphiques : si les chiffres présentés sont associés à la longueur ou à la hauteur des objets - des barres, dans ce cas - la longueur ou la hauteur doit être proportionnelle à ces chiffres. Il est donc conseillé de fixer la ligne de base du graphique à zéro.
Cette pratique consistant à ne pas faire commencer les axes à zéro nous permet d'exagérer l'ampleur visuelle d'une différence, même si elle n'est pas significative.
Pour intégrer ce concept dans notre bande dessinée, nous avons préféré utiliser une ligne continue plutôt que des barres, car nous voulions combiner plusieurs concepts.
Omission des données

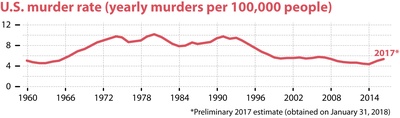
Pour la deuxième déconstruction, nous nous sommes à nouveau inspirés d'un graphique présenté dans Cairo A. (2019). Le graphique représente les taux d'homicides aux États-Unis (meurtres annuels pour 100 000 personnes) de 1960 à 2014.
Le graphique a été réalisé par Paul Krugman, un économiste et lauréat du prix Nobel, chroniqueur pour le New York Times. Une chose étonnante à constater est que le graphique s'arrête en 2014 alors que sa publication date de 2018. En approfondissant la question, voici ce qui en ressort. Plusieurs fois pendant la campagne présidentielle de 2016, mais aussi pendant sa première année de mandat, Donald Trump a mentionné une supposée hausse brutale des crimes violents aux États-Unis, en se concentrant notamment sur les meurtres. Il l'a reproché aux immigrants sans papiers, une affirmation qui a été démentie à plusieurs reprises. Krugman a affirmé que Trump avait tort et a utilisé à juste titre le graphique pour étayer ses propos. Examinons maintenant le graphique après avoir ajouté les quatre années manquantes.
Si le taux en 1970 est beaucoup plus faible qu'en 1990, on constate une augmentation dans les trois dernières années du graphique. Cette omission n'est pas anodine et est susceptible d'induire le lecteur en erreur. Il convient également de noter qu'il a été difficile de trouver exactement les données utilisées pour étendre le premier graphique, de sorte que les données ont été agrégées à partir du FBI, qui disposait de statistiques solides et précises pour 2016 et de chiffres préliminaires pour 2017. Ce graphique réel a servi de base à notre deuxième manipulation dans la caricature pour montrer que la tendance de la consommation de fromage est à la hausse, et que Schifaren n'a sélectionné que la courte période avec une tendance à la baisse.
Axes inversés
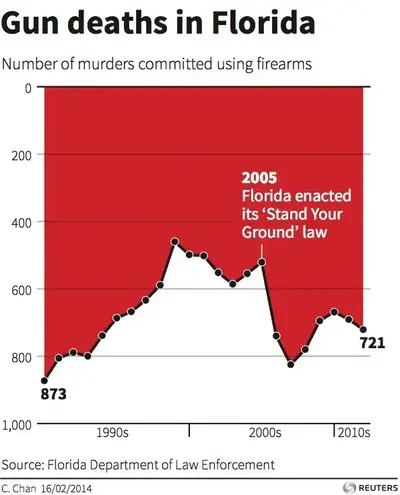
Pour ce dernier point, nous nous sommes inspirés du graphique suivant. Prenez un moment pour deviner ce qui ne va pas. A première vue, rien ne cloche, nous voyons un graphique qui monte et descend dans le sens où il y a beaucoup plus de morts par armes à feu dans les années 80 que maintenant. Les plus observateurs d'entre vous doutent déjà que cela ait quelque chose à voir avec la zone rouge représentée, peut-être certains auront-ils pris le temps de lire les chiffres écrits : on passe de 873 à 721 meurtres. Les axes sont ensuite inversés et regardons maintenant le tableau réel. Nous voyons que le nombre de décès a diminué. Nous avons donc pris ce graphique et l'avons intégré à notre histoire.
Points clés
-
Prendre le temps de bien regarder
- L'origine et limites des axes
- La direction des axes
- Est-ce-que les marquages sont également espacés ?
- Les données ont-elles l'air tronquées ou incomplètes ?
- Garder un regard critique sur les données et se rappeler qu'un graphe sert souvent pour appuyer un argument, et est donc rarement neutre ou objectif.
- Être conscients que des graphes mal faits sont présents partout dans notre quotidien.
Episode 3 - C'est pas sourcé !


La sorcière du village tente de vendre des potions aux coureur.euse.s du marathon, et elle a des preuves qu’elle fonctionne ! Il faut les yeux aguerris de Hugues pour dénicher des failles logiques dans son argumentaire, et nous donner une brève introduction aux études randomisées en double aveugle.
Extrapolation de données

La sorcière présente un graphe montrant la performance de participants suite à la consommation de potion. On pourrait poser la question des méthodes utilisées pour quantifier cette performance, mais cela sort du spectre de notre sujet. Ce qui est intéressant à voir, est que l’étude a été réalisée pour des volumes de potion allant jusqu’à une flasque. Ce basant sur ces éléments, et on observe bien une performance accrue dans ce régime.
Cependant, la sorcière affirme que cette tendance est continue et qu’alors trois flasques offrent “encore plus de performance”, ce que les données présentées ne permettent pas d’affirmer. Elle extrapole la tendance à la hausse sur une plage non étudiée, alors que celle-ci pourrait avoir un comportement différent, et pourrait notamment stagner ou même s’inverser.
Variables cachées et études randomisées
Si la tendance à la hausse dans l’étude peut être convaincante, le graphique ne suffit pas pour affirmer que la potion est à l’origine du gain de performance. Peut-être que les participant.e.s étaient déshydraté.e.s, et c’est l’eau dans la potion qui leur aurait permis de courir plus vite ; ou bien c’est le pic glycémique dû au sucre dans la potion. Une autre possibilité est que les participant.e.s étaient tellement convaincu.e.s de l’avantage qu’aurait la potion, qu’inconsciemment iels fournissent plus d’efforts en sachant l’avoir bue. Ce phénomène est communément appelé l'effet placebo.
Pour isoler ces variables, Hugues propose faire une étude randomisée en double aveugle. En donnant au hasard de l’eau sucrée ou de la potion aux participant.e.s, sans qu’iels sachent laquelle des deux iels reçoivent. De cette manière, on limite l’effet placebo. De plus, on s’assure en comparant la performance des deux groupes que l’effet est bien dû à la potion même, et pas dû à l’eau ou le sucre qu’elle contient.
Attention, petits échantillons !

Le but final de cette étude est d’estimer la performance moyenne attendue en ayant bu de la potion, et la comparer à celle de l’eau sucrée. On essaye en d’autres mots d’estimer les moyennes de chacune des deux distributions, que l’on échantillonne expérimentalement. Si la potion n’a pas d’effet (c’est l’hypothèse nulle), alors les distributions et les moyennes associées sont identiques.
Ce que présente la sorcière est alors la moyenne empirique, obtenue à partir des échantillons. Or il faut prendre en compte dans cette estimation une certaine incertitude, due au fait que les échantillons ne sont pas tous identiques, et sont chacun plus ou moins loin de la moyenne théorique. Cet écart à la moyenne est quantifié par la variance de la distribution.
Intuitivement, on imagine que plus la variance de la distribution est grande (c’est-à-dire les échantillons sont loin de la moyenne), plus il y aura d’incertitude sur la l’estimation. Et inversement, plus on récolte d’échantillons, meilleure elle sera.
Raymonde a alors observé que les échantillons ont une grande variabilité, et que cette variance est trop grande par rapport à la différence des deux moyennes estimées : impossible donc de dire si les deux distributions ont la même moyenne.
Pour pouvoir conclure, il faut donc diminuer l’incertitude sur les estimations de moyenne ; et comme on ne contrôle pas la variance des distributions, c’est donc le nombre d’échantillons qu’il faut augmenter.
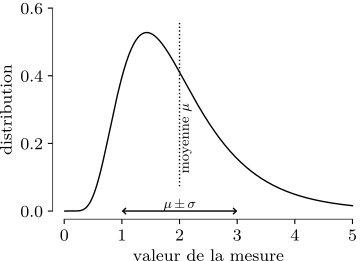

Mettons tout cela en application, et voyons comment les données ont été générées pour la planche :
- On définit la distribution des performances comme log-normale, de moyenne μ=2 et écart-type σ=1. La distribution est identique pour l’eau sucrée et la potion, donc ici on sait que la potion n’a pas d’effet. Notons que expérimentalement on n’a pas accès à ces paramètres !
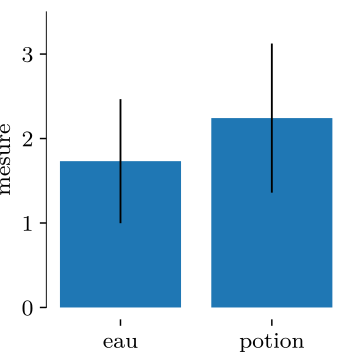
- On échantillonne cette distribution, dix fois pour chacun des deux groupes; le groupe contrôle, à qui on a donné de l'eau sucrée, et le groupe test, qui a reçu de la potion. On obtient les résultats suivants. Notons que le diagramme en bandes est peu efficace en termes de densité d’informations, puisqu’il ne montre que la moyenne estimée et l’écart-type des échantillons, sans montrer les données brutes.
- On calcule l’estimation de la moyenne (voir détails techniques) et l’incertitude. Pour les groupe contrôle, on trouve μ≈1.7±0.2, et pour le groupe test μ≈2.2±0.3.
- Si on s’en fie aux valeurs nominales, on pourrait penser que la potion fonctionne, et mène à des meilleures performances ! Or ces résultats sont dus purement à la chance, puisque les deux groupes sont échantillonnés à partir de la même distribution. Avec un si petit échantillon, les fluctuations aléatoires jouent un grand rôle, et il faut prêter attention aux incertitudes.
Voici la même expérience, répétée avec N=200 échantillons par groupe (avec des traits au lieu de croix, pour améliorer la lisibilité).
Points clés
- Ne pas extrapoler, surtout si on n’a pas de modèle théorique.
- Attention aux variables cachées. A quoi compare-t-on les données ?
- Toujours inclure une incertitude dans une mesure expérimentale, et tenir en compte l’incertitude lors de comparaisons.
- Montrer en priorité les données brutes. Un diagramme en bandes montre que la moyenne et l’écart type (estimés), et cache ainsi le détail.
- La taille de l’échantillon est importante ; plus est toujours mieux.
Notes techniques
Soit un distribution ayant pour moyenne μ et variance σ².
On échantillonne identiquement et indépendamment la distribution n fois, et on obtient les échantillons {x₁, …, xₙ}.
Alors on peut estimer la moyenne par m=1/n ∑xᵢ. Comme xᵢ sont des variables aléatoires, m l’est aussi, et on peut prouver que son écart type (l’incertitude) est σₘ=σ/√n. On note alors μ=m±σₘ. Expérimentalement on ne connaît pas σ, mais on peut l’estimer par σ≈s=√[1/(n-1) ∑(xᵢ-m)²].